티스토리 뷰
자료구조? Data Structure
: 컴퓨터에서 자료들을 정리하고 조직화 하는 여러 가지 구조
1. 자료구조의 분류

- 단순 자료구조 : 정수, 실수, 문자, 문자열 처럼 많은 프로그래밍 언어에서 기본적으로 제공하는 구조
- 복합 자료구조 : 여러가지 자료들이 복합적으로 구성됨
- 선형 구조 : 자료들이 순서적으로 나열(ex : stack, queue, dequeue)
- 순서 접근 : (ex : 연결 리스트)
- 직접 접근 : (ex : 배열)
- 비선형 구조 : 자료들 간에 선형적인 순서가 있는 것이 아니라 보다 복잡한 연결을 갖는 형태
- 트리 : 회사의 조직도나 컴퓨터의 폴더와 같은 계층 구조를 표현하기에 적합 , 이진 탐색 트리는 탐색에 적합(효율성을 높인 방법은 AVL 트리), 힙 구조는 트리의 중요한 응용중 하나
- 그래프 : 지하철 노선, SNS의 인맥 지도, 인터넷 망 등을 표현할 수 있는 가장 복잡한 형태의 자료구조
- 정점을 연결하는 간선의 방향성 유무에 따라 방향 그래프, 무방향 그래프
- 간선이 가중치를 가질 수 있으면 가중치 그래프 (ex : 신장 트리, 최단 경로)
- 선형 구조 : 자료들이 순서적으로 나열(ex : stack, queue, dequeue)
2. 자료구조의 활용
대표적인 사례는 정렬과 탐색
정렬 : 알고리즘 적 측면이 강하지만 효율적 정렬을 위해 다양한 자료구조의 활용이 필요함
탐색 : 적절한 자료구조와 그에 따른 알고리즘을 사용하는 경우 가장 효율적인 탐색이 가능
알고리즘 ?
사전에서 알파벳 순 나열을 이용해 단어를 찾는 것 처럼 어떤 문제를 해결하는데 효율적인 방법을 이용하는 절자
이런 문제 해결 절차는 프로그래밍 스타일이나 프로그래밍 언어와는 무관하다.
프로그램 = 자료구조 + 알고리즘
1. 알고리즘의 성능 분석
알고리즘을 코드로 직접 구현해 C언의 clock() 함수를 이용해 직접 실행시간을 측정해 볼 수 있다. 하지만 이러한 방식은 직접 구현해야 한다는 점, 동일한 조건의 하드웨어 상에서 비교가 이루어 져야 한다는 점, 동일한 언어를 사용해야 한다는 점에서에 알고리즘 성능 분석에 적절한 방법은 아니다.
<알고리즘 복잡도 분석(complexity analysis)>
알고리즘을 구현하지 않고도 모든 입력을 고려하는 방법, HW/SW 환경과 관계없이 알고리즘의 효율성을 분석할 수 있다
좋은 알고리즘 이란 ? : 실행시간이 빠르다 , 처리를 위한 기억공간이 적다.
- 시간 복잡도(time complexity) : 알고리즘의 실행 시간 분석
- 공간 복잡도(space complexity) : 알고리즘이 사용하는 기억 공간 분석
1.1. 시간 복잡도 함수
알고리즘을 이루고 있는 연산들(산술, 대입, 비교, 이동) 이 몇 번이나 실행되는지를 숫자로 표시
시간 복잡도 함수 ? : 연산의 수는 보통 입력 갯수 n 에 영향을 받는데, 연산의 수를 n을 이용해 함수로 표시한 것 T(n)
1.2. 빅오 표기법
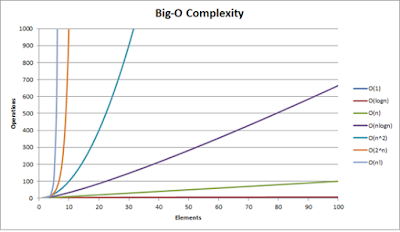
일반적으로 시간 복잡도 함수 T(n) 은 입력의 갯수 n에 대한 상당히 복잡 수식으로 나타남
그러나 자료의 갯수가 많아질 수록, 즉 n이 커질수록 T(n)에서 차수가 가장 큰 항의 영향력이 절대적으로 높아진다.
따라서 시간 복잡도 분석에서는 함수의 전체 항이 아니라 최고차항 만을 고려하면 된다.
시간 복잡도 함수에서 불필요한 정보를 제거하고 알고리즘 분석을 쉽게 할 목적으로 시간 복잡도를 표시하는 방법을 "빅오 표기법" 이라고 한다.
ex : T(n) = n^2 + n + 1 --> O(n^2)
f(n) = n^2 + n + 1
g(n) = c(n^2)
일 때 |n^2 + n + 1| <= c|n^2| 를 만족하는 c 가 존재한다면 T(n) = n^2 + n + 1 --> O(n^2)
1.3. 이 외의 표기법
빅오 표기법은 상한선에 제한이 없기 때문에 문제가 있다.
이러한 문제점을 보완하기 위한 빅오메가 와 빅쎄타 표기법이 있다
빅오메가 : 함수의 하한을 표시
ex : T(n) = n^2 + n + 1 --> Ω(n^2)
f(n) = n^2 + n + 1
g(n) = c(n^2)
일 때 |n^2 + n + 1| >= c|n^2| 를 만족하는 c 가 존재한다면 T(n) = n^2 + n + 1 --> Ω(n^2)
빅세타 : 빅오와 빅오메가의 함수가 같을 경우!
ex : T(n) = n^2 + n + 1 --> ( Ω(n^2) == O(n^2) ) --> Θ(n^2)
1.4. 최선, 평균, 최악의 경우
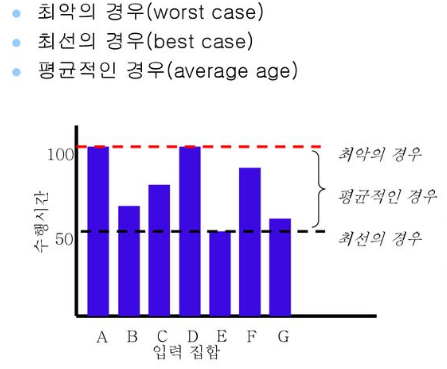
평균적인 실행시간이 가장 좋아보이지만 계산하기 어려운 경우가 많고, 최악의 상황을 보장해줄 수 없다는 단점이 있다.
따라서 알고리즘의 시간 복잡도로 최아그이 경우의 실행 시간이 가장 많이 쓰인다.
가령 비행기 관제 업무에 사용되는 알고리즘은 어떠한 입력에 대해서도 일정 시간 안에 반드시 계산을 끝내야 하기 때문에 최악의 경우를 사용하는 것이 알맞다.
'Algorithm > Data Structure' 카테고리의 다른 글
| 2. 스택(stack) (0) | 2019.11.27 |
|---|---|
| 1. 배열(Array) (0) | 2019.11.27 |
- Total
- Today
- Yesterday
- 객체지향
- Delete
- java
- select
- OOP
- .
- ojdbc6.jar
- JDBC 프로그램 작성단계
- view
- JdbcTemplate
- jdbc
- MVC
- Scott/Tiger
- 다형성
- Update
- 추상화
- model
- 객체
- INSERT
- 캡슐화
- java 환경설정
- 상속
- controller
- Oracle
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
